Describe the Shape of a Normal Probability Distribution

Approximately normal because ns006N and np1-P. This means that most of the observed data is clustered near the mean while the data become less frequent when.

Normal Probability Distribution An Overview Sciencedirect Topics

Mounded or unimodal U-shaped J-shaped reverse-J shaped and multi-modal.

. The distribution would have one peak and a long tail to the right. If there appear to be two mounds we say the distribution is bimodal. Symmetric skewed left or skewed right.

The distribution has no modes or no value around which the observations are. The distribution would have one peak and a long tail to the right. How would you describe the shape of the Normal Distribution.

It is Triangular in shape with the peak at u and a base width of 2o. Suppose that a coin is tossed 3000 times and 1800 heads result. The first distribution is unimodal it has one mode roughly at 10 around which the observations are concentrated.

That means the left side of the center of the peak is a mirror image of the right side. Here well concern ourselves with three possible shapes. The formula for the normal probability density function looks fairly complicated.

The normal distribution is the most commonly-used probability distribution in all of statistics. Approximately normal because ns005N and np1- 10. In this case we say that the distribution is skewed.

Common distribution shapes are listed here. Though we have three measures of central tendency they are not all appropriate for all situations. What does the shape of the data mean.

In general a mean refers to the average or the most common value in a collection of is. Choose the correct answer below. The distribution would have one peak and a long tail to the left.

The shape of the distribution cannot be ignored as it tells us which of the descriptive statistics we should be using. All of the above. But to use it you only need to know the population mean and standard deviation.

Choose the correct answer below. Statistics and Probability questions and answers a Describe the sampling distribution of Choose the phrase that best describes the shape of the sampling distribution below. A normal distribution is informally described as a probability distribution that is bell-shaped when graphed.

A distribution that is not symmetric must have values that tend to be more spread out on one side than on the other. Histograms and box plots can be quite useful in suggesting the shape of a probability distribution. If there are more than two mounds we say the distribution is multimodal.

Here well concern ourselves with three possible shapes. The normal distribution is a probability distribution so the total area under the curve is always 1 or 100. Describe the shape of a normal probability distribution.

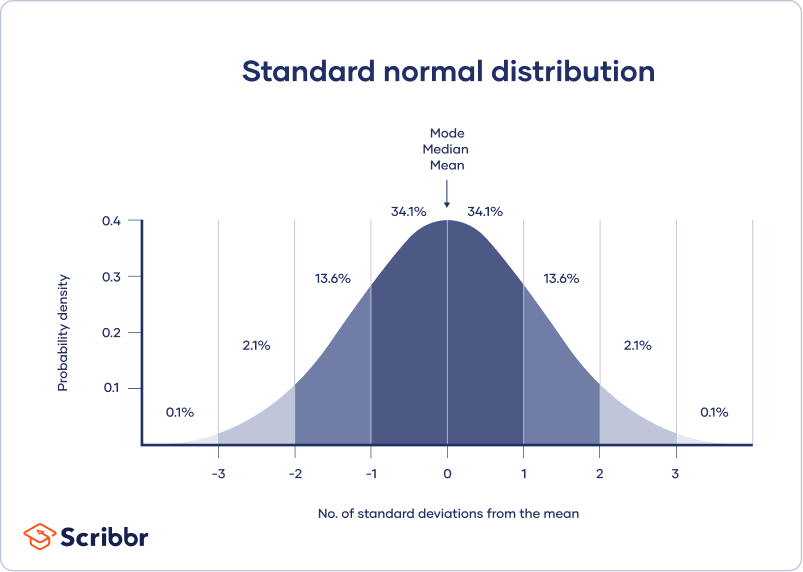
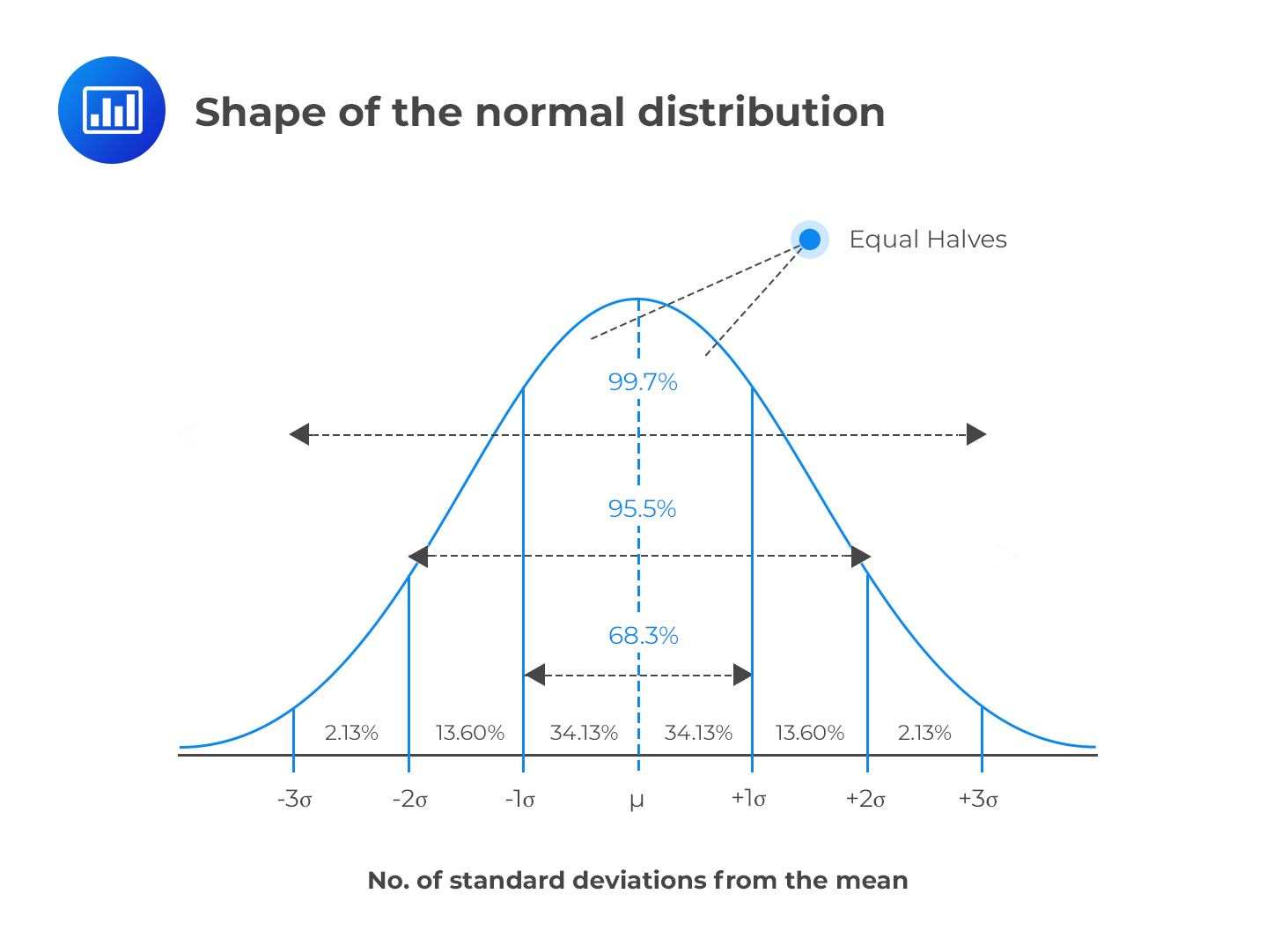
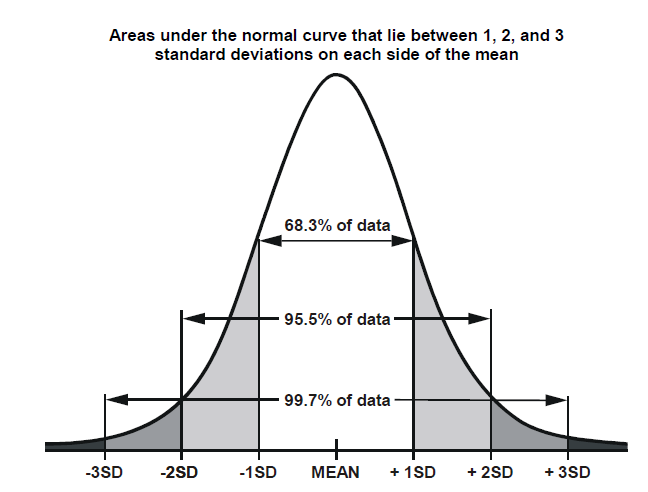
A normal distribution is symmetric from the peak of the curve where the mean Mean Mean is an essential concept in mathematics and statistics. Here is the percent chance of the various outcomes when you roll two dice. About 68 of data falls within one standard deviation of the mean.

It is Bell shaped and symmetrical with the center at u. It is rectangular in shape with limits at u-o and uo. The properties of the normal distribution are that its symmetrical mean and median are the same the most common values are near the mean and less common values are farther from it and the standard deviation marks the distance from the mean to the inflection point.

Figure 47 a Skewed to the left left-skewed. The distribution is roughly bell shaped. Unimodal it has one peak Mean and median are equal.

The third distribution is kind of flat or uniform. What is the empirical probability that a. First if the data values seem to pile up into a single mound we say the distribution is unimodal.

A bimodal distribution would have two high points rather than one. This is an example of a. It is Bell shaped with a long tail on the left side.

Measures of shape describe the distribution or pattern of the data within a. The density function of a normal probability distribution is bell shaped and symmetric about the mean. The sample size n is large.

The second distribution is bimodal it has two modes roughly at 10 and 20 around which the observations are concentrated. The distribution would have one peak and a long tail to the left. The Shape of a Distribution.

The essential characteristics of a normal distribution are. The single most important distribution in probability and statistics is the normal probability distribution. The shape of a distribution is sometimes.

Shape of the distribution. It is symmetric unimodal ie one mode and asymptotic. The normal distribution is the most important probability distribution in statistics because many continuous data in nature and psychology displays this bell-shaped curve when compiled and graphed.

For example if we randomly sampled 100 individuals we would expect to see a normal distribution frequency curve for many continuous variables such. The Normal bell-shaped distribution is probably the most well-known symmetric distribution. The distribution would depend on the values of the data.

The mean and median are less than the mode. The distribution is roughly bell shaped. It has the following properties.

The distribution would depend on the values of the data. The distribution is centered around the number seven and the probability decreases as you move away from the center. The binomial probability distribution tends to be bell-shaped when one or more of the following two conditions occur.

What is a measure of shape. Shape of Normal Distribution. If we plot the probability distribution and it forms a bell-shaped curve and the mean mode and median of the sample are equal then the variable has normal distribution.

Describe the shape of a normal probability distribution. A normal distribution is quite symmetrical about its center. Symmetric skewed left or skewed right.

Draw a rough sketch of a curve having the bell shape that is characteristic of a normal distribution. The normal distribution is the most important probability distribution in statistics because many continuous data in nature and psychology displays this bell-shaped curve when compiled and graphed. However the binomial probability distribution tends to be skewed when neither of these conditions occur.

Suppose that a coin is tossed 3000 times and 1800 heads result. The shape of a distribution will fall somewhere in a continuum where a flat distribution might be considered central and where types of departure from this include. 18 Practical Problems Related to Application of the Normal Probability Curve 19 Divergence in Normality The Non-Normal Distribution 110 Factors Causing Divergence in the Normal DistributionNormal Curve 111 Measuring Divergence in the Normal Distribution Normal Curve 1111 Measuring Skewness 1112 Measuring Kurtosis 112 Let Us Sum Up.

A good example of a bell curve or normal distribution is the roll of two dice. Both are located at the center of the distribution. We can characterize the shape of a data set by looking at its histogram.

The values of mean median and mode are all equal. The probability of success on a given trial p is close to 05. The normal probability distribution was introduced by the French mathematician Abraham de Moivre in 1733.

Normal Distribution Examples Formulas Uses

Key Properties Of The Normal Distribution Cfa Level 1 Analystprep

Why Is Normal Distribution Bell Shaped By Rishi Sharma Medium